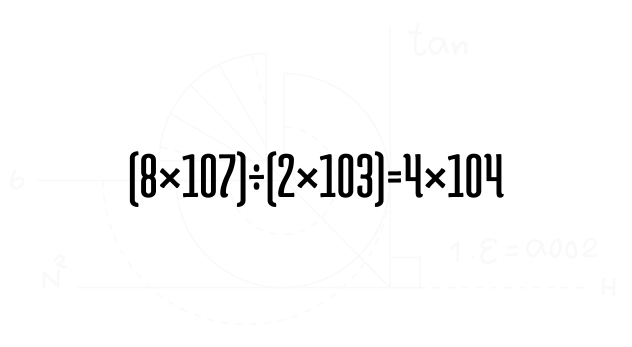¿Qué es la notación científica?
La notación científica es un método de representación matemática que se utiliza para expresar números muy grandes o muy pequeños de forma simplificada y fácil de manejar. Esta técnica emplea potencias de 10 para reducir la cantidad de cifras, facilitando cálculos y la interpretación de datos.
Estructura de la notación científica
La notación científica sigue la estructura general:
N=a×10nN = a \times 10^n
Donde:
a es el coeficiente, un número decimal mayor o igual a 1 y menor que 10.
10 es la base, que representa el sistema decimal.
n es el exponente, que indica cuántas posiciones se mueve el punto decimal.
Ejemplos de notación científica
1️⃣ Número grande: 3,600,000
3,600,000=3.6×1063,600,000 = 3.6 \times 10^6
2️⃣ Número pequeño: 0.00042
0.00042=4.2×10−40.00042 = 4.2 \times 10^{-4}
En el primer caso, el exponente es positivo porque el valor es mayor que 1.
En el segundo caso, el exponente es negativo porque el valor es menor que 1.
¿Cómo convertir un número a notación científica?
Pasos para la conversión:
1️⃣ Identificar el punto decimal en el número original.
2️⃣ Mover el punto decimal hasta que el número quede entre 1 y 10.
3️⃣ Contar los espacios movidos y asignar ese valor al exponente:
Si se movió hacia la izquierda, el exponente es positivo.
Si se movió hacia la derecha, el exponente es negativo.
Ejemplo práctico:
Convertir 52,000 a notación científica.
El número original es 52,000.
Movemos el punto decimal 4 posiciones a la izquierda → 5.2.
El exponente será 4 porque se movió hacia la izquierda.
52,000=5.2×10452,000 = 5.2 \times 10^4
Operaciones con notación científica
Suma y resta
Para sumar o restar en notación científica, los exponentes deben ser iguales. Si no lo son, es necesario ajustarlos.
Multiplicación
Se multiplican los coeficientes y se suman los exponentes:
(3×105)×(2×103)=6×108(3 \times 10^5) \times (2 \times 10^3) = 6 \times 10^{8}
División
Se dividen los coeficientes y se restan los exponentes:
(8×107)÷(2×103)=4×104(8 \times 10^7) \div (2 \times 10^3) = 4 \times 10^4
Aplicaciones de la notación científica
La notación científica se utiliza en múltiples áreas:
Ciencias naturales: para expresar distancias astronómicas y tamaños microscópicos.
Física: para representar la velocidad de la luz (3 × 10⁸ m/s) o la masa de un átomo.
Química: para trabajar con cantidades muy pequeñas de sustancias (1 mol ≈ 6.022 × 10²³ átomos).
Economía: para expresar cifras monetarias en millones o billones.
Conclusión
La notación científica es una forma eficiente y organizada de representar cantidades extremas de una manera comprensible y fácil de manipular. Su uso facilita los cálculos y reduce el riesgo de errores al manejar números de gran magnitud o muy pequeños.
