¿Qué son las leyes de los signos?
Las leyes de los signos son reglas matemáticas que permiten determinar el signo (positivo o negativo) del resultado al realizar operaciones como suma, resta, multiplicación o división con números con signo. Estas leyes son fundamentales en aritmética y álgebra, y forman la base para resolver expresiones y ecuaciones correctamente.
Importancia de comprender estas leyes
Dominar las leyes de los signos es esencial para:
Resolver operaciones básicas con números enteros
Trabajar con expresiones algebraicas
Resolver ecuaciones e inecuaciones
Evitar errores comunes en cálculos matemáticos
Un error en los signos puede alterar por completo el resultado de una operación, por lo que su correcta aplicación es clave en cualquier nivel educativo.
Leyes de los signos en la multiplicación y división
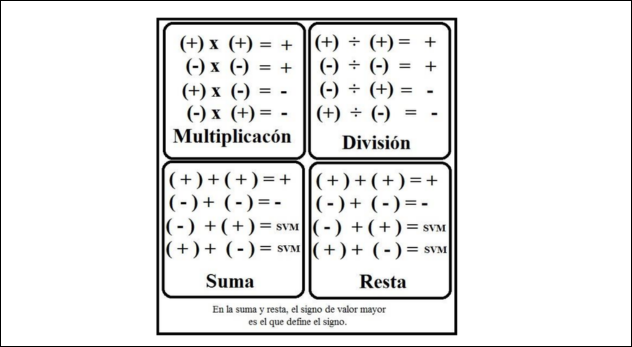
En las operaciones de multiplicación y división, las leyes de los signos son muy claras y consistentes:
Signos iguales dan positivo:
(+) × (+) = +
(–) × (–) = +
(+) ÷ (+) = +
(–) ÷ (–) = +Signos diferentes dan negativo:
(+) × (–) = –
(–) × (+) = –
(+) ÷ (–) = –
(–) ÷ (+) = –
Estas reglas también se aplican a productos y cocientes con más de dos factores. Si hay un número par de signos negativos, el resultado es positivo; si hay un número impar de signos negativos, el resultado es negativo.
Leyes de los signos en la suma y la resta
En la suma y resta, el proceso depende del valor absoluto y del signo de cada número:
Suma de números con el mismo signo:
Se suman los valores absolutos y se conserva el signo.
Ejemplo: (–5) + (–3) = –8Suma de números con distinto signo:
Se restan los valores absolutos y se conserva el signo del número con mayor valor absoluto.
Ejemplo: (+6) + (–10) = –4Resta de números:
Restar un número es lo mismo que sumar su opuesto.
Ejemplo: 7 – (–2) = 7 + 2 = 9
Estas reglas requieren atención, pero con práctica se vuelven intuitivas.
Aplicación en álgebra
En álgebra, las leyes de los signos se aplican constantemente al:
Resolver expresiones algebraicas
Multiplicar o dividir términos algebraicos
Desarrollar productos notables
Aplicar la factorización y simplificación de expresiones
Son también la base para resolver ecuaciones lineales, cuadráticas y sistemas de ecuaciones correctamente.
Conclusión
Las leyes de los signos son una herramienta indispensable para realizar operaciones matemáticas con precisión. Comprender y aplicar estas reglas con seguridad permite avanzar en el estudio del álgebra, la aritmética y otras ramas de las matemáticas sin errores comunes. Son el primer paso hacia una comprensión profunda del razonamiento lógico y numérico.